Jensen's Inequality

定義

  • 假設二維座標平面上 f(x) 是一個 convex function ( 凹向上、凸函數 ) ， E 代表期望值函數，那將會有以下性質：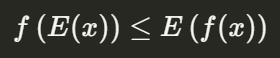

    • 對 x 先取期望值然後再把結果帶入 f 的結果，會 小於等於 先把 x 帶入 f 之後再取期望值的結果。

  • 假設二維座標平面上 f(x) 是一個 concave function ( 凹向下、凹函數 ) ， E 代表期望值函數，那將會有以下性質：

    • 對 x 先取期望值然後再把結果帶入 f 的結果，會 大於等於 先把 x 帶入 f 之後再取期望值的結果。

證明

  • 先討論 convex function 的情況。

    • 我們把 x 的期望值代入 f ，得到點 A ：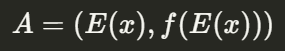

    • 接著把 f 上過點 A 的切線方程式叫做 T 。可以把點 A 帶入 f 的微分式，進而得到斜率，在有斜率且有已知點 A 的條件下，我們可以求出切線方程式 T ：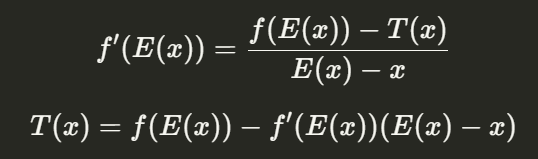

    • 接著利用 convex function 的特性， convex function 上某點 P=(m, n) 的 切線方程式 上的所有 y 座標值必定會小於等於在相同 x 座標值時 convex function 所對應到的 y 座標值：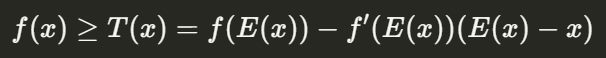

    • 兩邊取期望值，化簡後即可得證：

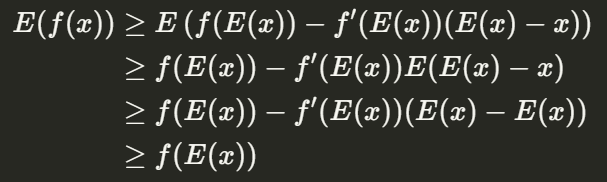
  • concave function 的情況也可以用類似的方法證明出來。