Randomized Algorithms
Randomized Algorithms
這邊是我對 Randomized Algorithms 的一些筆記與理解。
Lecture 01 : Events and Probability
Outline
Experiment ( 試驗 ) and Sample Space ( 樣本空間 )
Events ( 事件 ) and Probability ( 機率 )
Union Bound ( 布式不等式 )
Experiment
A process to produce an outcome.
Random Experiment
Experiment whose outcome is not known until the process is done.
Sample Space
The set of all outcomes of an experiment.
Events
A subset of the sample space.
Probability
A function Pr to measure the chance for each event to occure.
基本性質如下:
某事件 \(E\) 發生的機率必定大於等於 \(0\) :
\[ 1 \geq Pr(E) \geq 0 \]
若事件 \(\Omega\) 就是整個樣本空間的話,那發生的機率必定等於 \(1\) :
\[ Pr( \Omega ) = 1 \]
Union Bound
對於事件 \(E\) 與 \(F\) ,其聯集事件之機率小於等於 \(E\) 事件機率加上 \(F\) 事件機率:
\[ Pr(E \cup F) \leq Pr(E) + Pr(F) \]
用文氏圖畫出來理解的話如下:
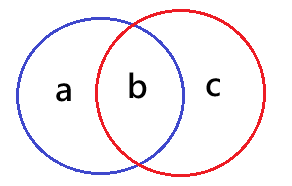
假設上圖中藍色事件代表事件 \(E\) 發生的機率,紅色的事件代表事件 \(F\) 發生的機率,那我們就可以推得 \(a+b+c = Pr(E \cup F)\) 、 \(a + b = Pr(E)\) 以及 \(b + c = Pr(F)\) ,又 \(a+b+c \leq a+b+b+c\) ,故 \(Pr(E \cup F) \leq Pr(E) + Pr(F)\)
Lecture 02 : Verifying Polynominal Identities ( 多項式恆等式 )
Outline
Checking Polynominal Identities
Conditional Probability ( 條件機率 ) & Independent Events ( 獨立事件 )
Sampling with/without Replacement ( 取後放回與取後不放回的抽樣 )
Checking Polynominal Identities
這邊要探討的問題大概可以想程如何測驗一個經過因式分解的多項式 \(F(x)\) 與一個被展開的多項式 \(G(x)\) 是不同或相同的多項式。
若要精確地證明,時間複雜度可能會有點大,若我們隨機產生出一個數字 \(c\) ,代入得 \(F(c)\) 與 \(G(c)\) ,用這個 \(c\) 所得到的結果來 "代表" 說我們現在認為 \(F(x)\) 是否等於 \(G(x)\) ,驗證一次的時間複雜度相比於之前的精確比對來得小。
不過上述隨機方法也不能完全表示兩者一定相等,我們需要一個可以衡量目前隨機的方法的錯誤率的方法。
當實際情況是 \(F(x)\) 不等於 \(G(x)\) 的時候,那 \(F(c) = G(c)\) 或者說 \(F(c) - G(c) = 0\) 的時候,該 \(c\) 就是一個 bad number ,也可以想成當 \(c\) 為 \(F(x) - G(x) = 0\) 的其中一根時,此時的 \(c\) 就是一個 bad number 。
這樣來看的話,如果 \(F(x) - G(x) = 0\) 是一個 \(d\) 次多項式的等式,那最多就會有 \(d\) 個 bad number ,而我們也可以說 \(Pr(error) \leq \frac{d}{n}\) 。
Conditional Probability
假設 \(E\) 和 \(F\) 為兩事件,且 \(Pr(F) > 0\) ,那在 \(F\) 發生的條件下 \(E\) 發生的機率可以記做 \(Pr(E|F) = \frac{Pr(E \cap F)}{Pr(F)}\) 。
Independent Events
當事件 \(E\) 和 \(F\) 互為獨立事件時,我們可以寫出條件機率的式子為 \(Pr(E|F) = Pr(E)\) 。
可以帶入 Conditional Probability 的公式,經過運算可以得到把上面的 \(Pr(E|F)\) 換成 \(\frac{Pr(E \cap F)}{Pr(F)}\) ,這樣一來我們就可以得到 \(Pr(E \cap F) = Pr(E)Pr(F)\) 。
思考可以如何改善或縮小使用隨機的方式來檢測 Polynominal Identities 的錯誤率 ( \(Pr(error)\) )
可能的做法 1 :增加檢測的隨機數的範圍。我們可以知道 \(Pr(error) \leq \frac{d}{n}\) ,當 \(n\) 越大 \(Pr(error)\) 的機率的最大值就會越小。不過這個方法在產生很大的範圍的隨機數時,可能會需要相當大的資源需求。
可能的做法 2 :跑多次隨機演算法。雖然隨機範圍沒有變大,但是 \(Pr(error)\) 仍然會變小,下面為跑 \(k\) 次隨機演算法的情況下的寫法,這邊避免寫太長所以 \(error\) 就先用 \(e\) 表示:
\[ \begin{aligned} Pr(e) &= Pr(e_1 \cap e_2 \cap \dots \cap e_k) \\ &= Pr(e_1)Pr(e_2|e_1)Pr(e_3| e_1 \cap e_2 ) \dots Pr(e_k|e_1 \cap e_2 \cap \dots \cap e_{k-1}) \end{aligned} \]
Sampling with/without Replacement
這邊剛好可以接續前面跑多次隨機演算法的例子來解釋。
開始之前先設 \(e=error\) 。首先,我們有了 \(Pr(e) = Pr(e_1)Pr(e_2|e_1)Pr(e_3| e_1 \cap e_2 ) \dots Pr(e_k|e_1 \cap e_2 \cap \dots \cap e_{k-1})\) 這個式子;接著我們分成兩種情況,第一種情況就是每次出現的隨機數之後必定不會再出現 ( 取後不放回 ) ,第二種情況就是每次出現的隨機數之後有可能還會再出現 ( 取後放回 ) 。
分析第一種情況下的 \(Pr(e)\) :
\[ Pr(e) \leq \frac{d}{n} \times \frac{d-1}{n-1} \times \frac{d-2}{n-2} \times ... \times \frac{d-k+1}{n-k+1} \]
分析第二種情況下的 \(Pr(e)\) :
\[ Pr(e) \leq \left ( \frac{d}{n} \right )^k \]
我們可以大致看出,跑多次隨機演算法的情況下 \(Pr(e)\) 的最大值會越來越小,並且可以理解到取後放回與取後不放回的差異。
Lecture 03 : Verifying Matrix Multiplication ( 矩陣乘法 ) , Randomized Min-Cut ( 最小割 )
Outline
Law of Total Probability ( 全機率定理 )
Principle of Deferred Decision ( 延遲決策原則 ( 不太確定是不是這樣翻 ) )
Verifying Matrix Multiplication
Randomized Min-Cut
Law of Total Probability
假設事件 \(E_1, E_2, \dots , E_k\) 為某樣本空間的所有事件分割,那該樣本空間的任意事件 \(B\) 有以下性質:
\[ \begin{aligned} Pr(B) &= Pr(B \cap E_1) + Pr(B \cap E_2) + \dots + Pr(B \cap E_k) \\ &= Pr(B|E_1)Pr(E_1) + Pr(B|E_2)Pr(E_2) + \dots + Pr(B|E_k)Pr(E_k) \\ &= Pr(E_1|B)P(B) + Pr(E_2|B)P(B) + \dots + Pr(E_k|B)P(B) \end{aligned} \]
Principle of Deferred Decision
先固定結果的部分,再固定剩餘的部分。
上述說法可能會有點抽象,下面會有一些舉例。
舉例一:擲一個公正的骰子 \(10\) 次,則 \(Pr( sum \space is \space divisible \space by \space 6 )\) 為多少?
普通作法可能就是檢查所有 \(6^{10}\) 種結果,但是這個方法似乎太麻煩了。
這邊我先假設 \(Pr(Ans) = Pr( sum \space is \space divisible \space by \space 6 )\) ,來簡化後面的表達式。
使用了 Deferred Decisions 的作法就會像是先假設我們已經擲了 \(9\) 次骰子,又設 \(S\) 為擲 \(9\) 次中所可能產生的 \(6^9\) 種事件的 其中一種 ,從這邊我們可以推得 \(Pr( Ans \space | \space S) = \frac{1}{6}\) ,這是因為如果我們已經擲了 \(9\) 次骰子,那到這邊代表前九次的總和已經是 定值 ,那最後一個骰子要剛好出現剛好能補到可以被六整除的值的機率就是 \(\frac{1}{6}\) ,因為一定是六個數字選一個數字來補。
接著可以嘗試把 \(Pr( Ans )\) 套用 Law of Total Probability 去把式子展開,並且套用我們先前推倒出的結論,這樣就可以算出 \(Pr( Ans )\) 了:
\[ \begin{aligned} Pr(Ans) &= \sum_S \left ( Pr(Ans|S)Pr(S) \right ) \\ &= \frac{1}{6} \sum_S \left ( Pr(S) \right ) \\ &= \frac{1}{6} \times 1 \\ &= \frac{1}{6} \end{aligned} \]
舉例二:把 \(1\) 個公正的硬幣混入 \(9\) 個不一定公正的硬幣中,硬幣皆有正反兩面,我們能做到在無法得知公正硬幣是哪一枚時,用這 \(10\) 個硬幣 "模擬" 出一個公正的硬幣嗎?
答案是可以的,我們可以利用出現的正面是否為奇數來作辨別 ( 這邊假設出現正面次數為偶數的事件代表模擬出正面 ) ,做法如下。
設 \(Pr(Ans) = Pr(positive \space is \space even)\) 。
這邊要做的東作跟前面擲骰子那題類似,也就是拆成 \(1\) 個公正硬幣和 \(9\) 個不一定公正硬幣的情況來看,而 \(9\) 個不同硬幣所產出的所有結果的 其中一種 我設其為 \(S\) ,一樣可以視 \(S\) 為 定值 ,我們的公正硬幣一定要二選一才可以讓結果符合 \(Pr(Ans)\) ,這樣我們就可以推得 \(Pr( Ans \space | \space S) = \frac{1}{2}\) 。
展開 \(Pr(Ans)\) 就可以得出答案為 \(\frac{1}{2}\) ,即模擬出一個公正硬幣:
\[ \begin{aligned} Pr(Ans) &= \sum_S \left ( Pr(Ans|S)Pr(S) \right ) \\ &= \frac{1}{2} \sum_S \left ( Pr(S) \right ) \\ &= \frac{1}{2} \times 1 \\ &= \frac{1}{2} \end{aligned} \]
Verifying Matrix Multiplication
這邊要探討矩陣乘法相關的問題。
假設我們有 \(3\) 個 \(n \times n\) 的矩陣 \(A, B, C\) ,我們要驗證是否 \(AB=C\) 。
與先前提到的 ( Checking Polynominal Identities ) 類似,若要精確地證明,時間複雜度可能會有點大,所以這邊採用隨機的做法。
使用一個隨機的 \(1 \times n\) 的 bit 矩陣 \(v\) ,也就是說其元素只會有 \(0\) 或者 \(1\) 這兩種可能,並且計算 \(ABv\) 與 \(Cv\) ,如果兩者的值相等,那我們就直接說 \(AB=C\) 。
如果採用上述做法,那時間複雜度就會是 \(O(n^2)\) ,因為 \(Cv\) 運算會需要 \(O(n^2)\) ,在計算 \(ABv\) 時如果先計算 \(u=Bv\) 再算 \(Au\) 那也會需要 \(O(n^2)\) ,這樣整個演算法就只需要 \(O(n^2)\) 這樣的時間複雜度。
接下來要討論 bad random \(v\) 的情況,因為就算 \(ABv=Cv\) 也不一定代表 \(AB=C\) ,這是因為 \(ABv=Cv\) 可看成 \((AB-C)v=0\) ,而 \(AB-C\) 不一定是零矩陣。
我們假設 \(D=AB-C\) ,且 \(D\) 存在的其中一個非零元素為 \(d_{xy}\) , \(x\) 代表第幾列, \(y\) 代表第幾行。
我們要討論在 \(Dv=0\) 的時候 \(D\) 不一定等於零矩陣,用上述的 \(d_{xy}\) 列出的等式如下:
\[ d_{x1}v_1 + d_{x2}v_2 + \dots + d_{xy}v_y + \dots + d_{xn}v_n = 0 \]
又 \(d_{xy}\) 非零,故可知道 \(v_y\) 如下:
\[ v_y = \frac{d_{x1}v_1 + d_{x2}v_2 + \dots + d_{xn}v_n}{d_{xy}} \]
接著要來計算我們有多大的機率會得到 bad random \(v\) ,也就是 \(Pr(error)\) ,可以先列出以下算式:
\[ Pr(error) = Pr(Dv=0) \]
上述 \(0\) 代表每列都為零,這個機率一定會小於等於只需要一列為零的機率,所以又可以列式如下:
\[ \begin{aligned} Pr(error) &= Pr(Dv=0) \\ & \leq Pr \left (v_y = \frac{d_{x1}v_1 + d_{x2}v_2 + \dots + d_{xn}v_n}{d_{xy}} \right ) \end{aligned} \]
我們可以利用 Deferred Decision 先把除了 \(v_y\) 的其他元素固定住,其所有組合的其中一種叫做 \(S\) ,這樣我們就可以推得一下方 \(RHS\) ( Right Hand Side ) 是一個固定值:
\[ RHS = \frac{d_{x1}v_1 + d_{x2}v_2 + \dots + d_{xn}v_n}{d_{xy}} \]
到這邊我們可以知道,此時 \(RHS\) 是一個定值,在發生事件 \(S\) 的條件下,且發生 \(v_y = RHS\) 的機率 ( \(Pr( v_y = RHS \space | \space S)\) ) 不會超過 \(\frac{1}{2}\) ,這是因 \(v\) 是 bit 矩陣,如果 \(RHS\) 剛好等於 \(0\) 或 \(1\) ,那麼這時 \(Pr( v_y = RHS \space | \space S) = \frac{1}{2}\) ,如果不是 \(0\) 或 \(1\) 這兩個數值時 \(Pr( v_y = RHS \space | \space S) = 0\) ,故我們可以寫出機率算式如下:
\[ Pr( v_y = RHS \space | \space S) \leq \frac{1}{2} \]
結合前面所提到的算式得出 \(Pr(error)\) 的不等式如下:
\[ \begin{aligned} Pr(error) &= Pr(Dv=0) \\ & \leq Pr \left (v_y = \frac{d_{x1}v_1 + d_{x2}v_2 + \dots + d_{xn}v_n}{d_{xy}} \right ) \\ & \leq \frac{1}{2} \end{aligned} \]
Randomized Min-Cut
這邊要探討的問題是 Min-Cut 的求法,會先大致說明移下 Min-Cut 為何,我會把這邊參考的資料放在參考資源那邊。
要理解 Min-Cut 還要先了解何謂 S-T Cut 。
假設我們把一個由節點 ( node ) 和附帶權重 ( weight ) 的邊 ( edge ) 構成的有向圖 \(G\) ,分成兩個子集合 \(S\) 與 \(T\) ,且有以下性質:
\[ \begin{aligned} S \cup T = V \\ S \cap T = \emptyset \\ s \in S \\ t \in T \end{aligned} \]
\((S, T)\) 就叫做 S-T Cut ,並且可以想像東西在 \(s\) 與 \(t\) 這兩個 node 之間做流動。
\(Capacity(S, T)\) 為所有離開 \(S\) 的邊的權重和。
而所謂的 Min-Cut 也就是滿足使 \(Capacity(S, T)\) 最小的 \((S, T)\) 。 Min-Cut 不一定只有一種。
以上就大改說明了一下何謂 Min-Cut 。
現在要來說明我們這邊要處理的 Min-Cut Problem 的定義,我們這邊使用一個無向圖 \(G\) ,其邊無相異權重,我們要求的是一個需要最少邊的 S-T Cut ,解設我們有 \(n\) 個節點與 \(m\) 個邊。這樣的定義其實也只是原先描述的 Min-Cut 初始情境的特例。
這邊我們使用的演算法大致像這樣:只要 \(G\) 還剩下大於 \(2\) 個節點,我們就會從 \(G\) 裡面隨機挑一個邊 \(e\) 出來,把 \(e\) 這個邊收縮,也可以想成把 \(e\) 兩端的節點融合,之後去除掉所有節點上的 self-loop ,重複前述做法值到 \(G\) 的節點數,小於等於 \(2\) ,而最後所剩下的邊的集合 ( 就像是前面所述的 \((S, T)\) ,可看成連接於兩個最終頂點的邊 ) 就可以視為是我們想要求的 Min-Cut 。
由於 Min-Cut 不一定只有一種,我們可以得到這樣一個結論,對於 特定一種 Min-Cut \(C\) 來說,在執行隨機演算法的過程中如果沒有任何一個 \(C\) 裡面的邊被收縮 ( edges of \(C\) not contracted ) ,那最終答案就會是 \(C\) ,而我們也可以知道我們的隨機演算法要做出正確判斷的機率 \(Pr(correct)\) 至少會等於沒有任何一個 \(C\) 裡面的邊被收縮的機率 ( 因為可能還會有其他也可以是 Min-Cut 的事件 \(C\) ) ,也就是下面的算式:
\[ Pr(correct) \geq Pr( edges \space of \space C \space not \space contracted ) \]
現在要來 bound \(Pr( edges \space of \space C \space not \space contracted )\) 這個值,由於 \(edges \space of \space C \space not \space contracted\) 這個事件是每次隨機選都不選到 \(C\) 裡面的邊,我們設 \(E_j\) 代表第 \(j\) 輪 ( \(j\) 從 \(1\) 開始 ) 隨機選的時候不選到 \(C\) 裡面的邊的機率,設 \(Pr(X)=Pr( edges \space of \space C \space not \space contracted )\) ,可以先列出以下算式:
\[ \begin{aligned} Pr(X) &= Pr(E_1 \cap E_2 \cap \dots \cap E_{n-2}) \\ &= Pr(E_1)Pr(E_2|E_1)Pr(E_3|E_1 \cap E_2) \dots Pr(E_{n-2}|E_1 \cap E_2 \cap \dots \cap E_{n-3}) \end{aligned} \]
接著我們假設 \(|C|=k\) ,可以理解成 \(C\) 包含了 \(k\) 個邊,我們可以知道任何一個節點的 degree ( 連接的邊的個數 ) 一定會大於或等於 \(k\) ,而由這個結論我們還可以知道在第 \(j\) 輪的時候 \(G\) 的總邊數的不等式:
\[ edges \space in \space G \geq \frac{(n-(j-1))k}{2} = \frac{(n-j+1)k}{2} \]
將上式帶入先前得出的 \(P(X)\) 公式 ( \(Pr( edges \space of \space C \space not \space contracted )\) ) :
\[ \begin{aligned} Pr(X) &= Pr(E_1 \cap E_2 \cap \dots \cap E_{n-2}) \\ &= Pr(E_1)Pr(E_2|E_1)Pr(E_3|E_1 \cap E_2) \dots Pr(E_{n-2}|E_1 \cap E_2 \cap \dots \cap E_{n-3}) \\ & \geq \left ( 1-\frac{k}{\frac{(n-1+1)k}{2}} \right ) \left ( 1-\frac{k}{\frac{(n-2+1)k}{2}} \right ) \left ( 1-\frac{k}{\frac{(n-3+1)k}{2}} \right ) \times \dots \times \left ( 1-\frac{k}{\frac{(n-(n-2)+1)k}{2}} \right ) \\ & \geq \left ( \frac{n-2}{n} \right ) \left ( \frac{n-3}{n-1} \right ) \left ( \frac{n-4}{n-2} \right ) \times \dots \times \left ( \frac{1}{3} \right ) \\ & \geq \left ( \frac{n-2}{n} \right ) \left ( \frac{n-3}{n-1} \right ) \left ( \frac{n-4}{n-2} \right ) \times \dots \times \left ( \frac{2}{4} \right ) \left ( \frac{1}{3} \right ) \\ & \geq \left ( \frac{1}{n} \right ) \left ( \frac{1}{n-1} \right ) \left ( \frac{1}{1} \right ) \times \dots \times \left ( \frac{2}{1} \right ) \left ( \frac{1}{1} \right ) \\ & \geq \frac{2}{n(n-1)} \end{aligned} \]
再帶回更前面的式子可以得到:
\[ Pr(correct) \geq Pr( edges \space of \space C \space not \space contracted ) \geq \frac{2}{n(n-1)} \]
Lecture 03-S : Karger and Stein's Speed Up
Outline
With High Probability
Karger and Stein's Speed Up
With High Probability
架設整個樣本空間的大小為 \(n\) ,如果有一件事情 \(E\) 發生的機率至少是 \(1-\frac{1}{n^c}\) ,其中 \(c\) 為某個正常數,那我們就可以說 \(E\) happens with high probability 。
這邊用 With High Probability 的觀念來回顧一下先前我們實做 Randomized Min-Cut :
\[ P(correct) \geq \frac{2}{n(n-1)} \]
執行 \(t\) 次至少有一次成功機率如下:
\[ P(correct) \geq 1-(1-\frac{2}{n(n-1)})^t \]
設 \(t=n(n-1)\ln(n)\) ,並且利用 \(1+x \leq e^x\) 這個不等式之後可以得到以下結果:
\[ \begin{aligned} P(correct) & \geq 1- \left ( 1-\frac{2}{n(n-1)} \right )^{n(n-1)\ln(n)} \\ & \geq 1-\frac{1}{n^2} \end{aligned} \]
Karger and Stein's Speed Up
會有 Contract() ,把 \(G\) 收縮到大約剩下 \(\frac{n}{\sqrt{2}}\) 個節點,也可以說收縮到 \(Pr(all \space contraction \space is \space "good") = \frac{1}{2}\) 。
整個演算法大致如下:
1 | MinCut(G) { |
經過推導之後可以得到一個較先前的 \(Pr(correct) \geq \frac{2}{n(n-1)}\) 更好的不等式,這邊先用 \(f(a)\) 來代表樣本空間為 \(a\) 的情況:
\[ f(a) \geq 1 - \left ( 1- \frac{1}{2} f \left ( \frac{a}{\sqrt{2}} \right ) \right )^2 \]
解完上述遞迴可以得到:
\[ f(n) = Pr(correct) \geq \frac{1}{\log (n)} \]
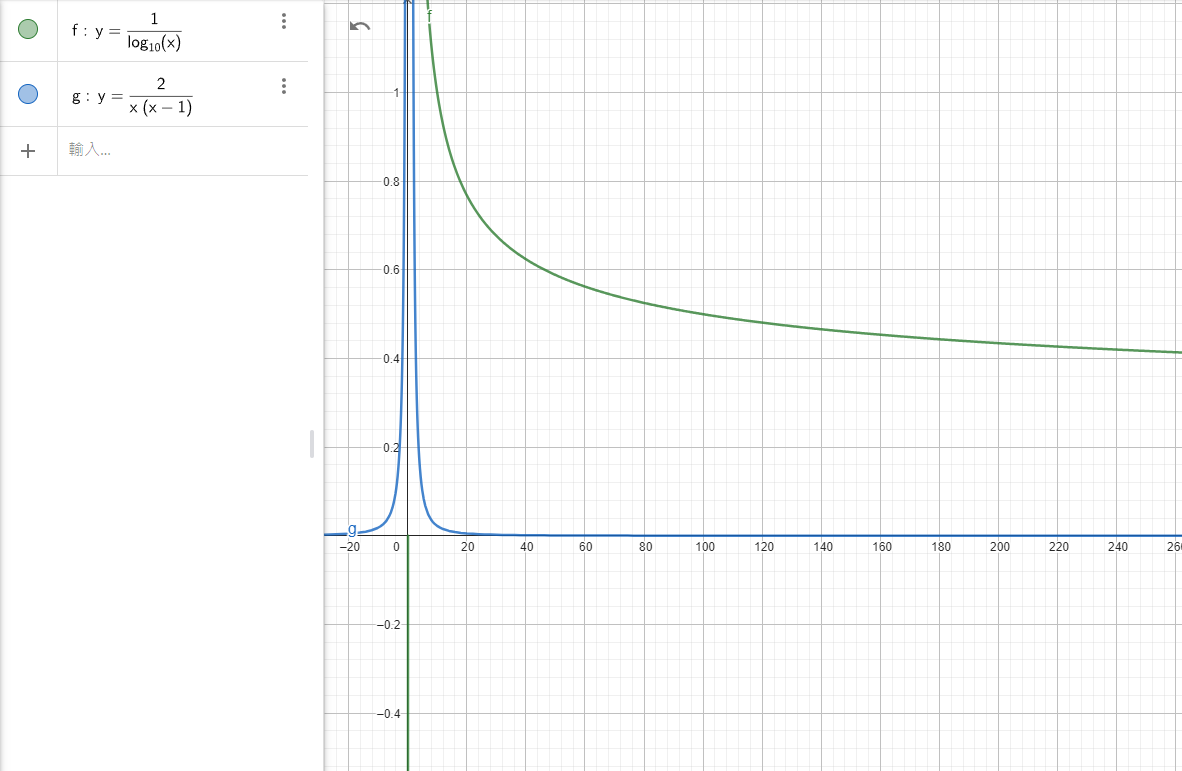
我們得到界線為 \(\frac{1}{\log (n)}\) ,而這個界線比之前沒有用 Karger and Stein's Speed Up 時的 \(\frac{2}{n(n-1)}\) 還要來得更好,下圖為比較圖:
 |
|---|
| 此圖使用 這個工具 來繪製 |
參考資源
1 | 隨機演算法: |

